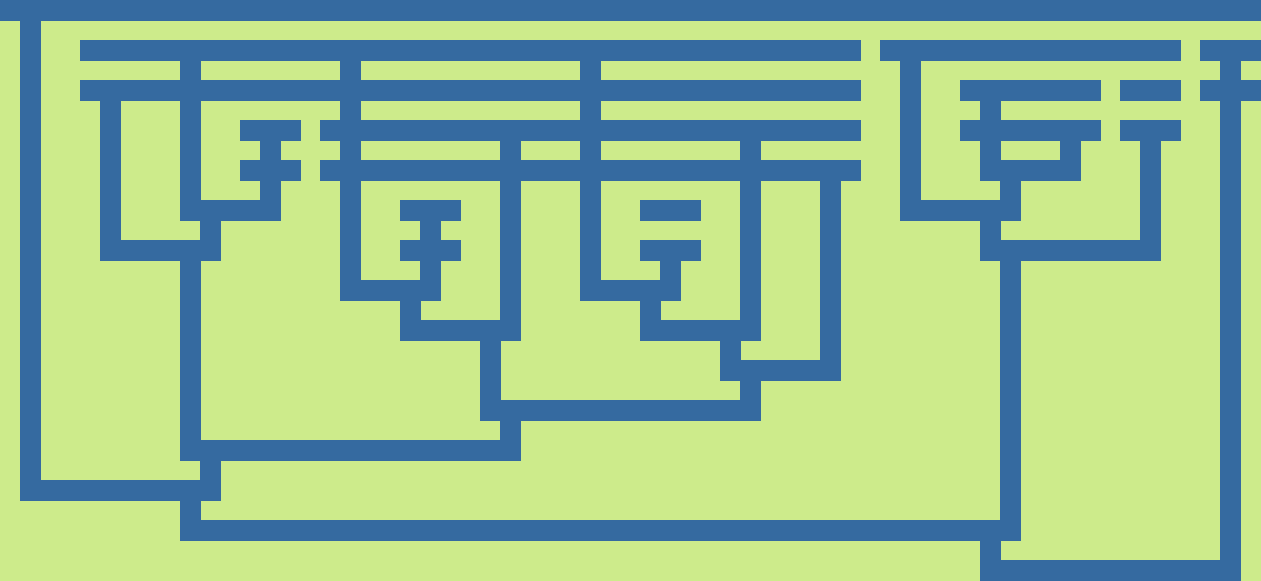
Fibonacci function, modified alternative (short-application) style

29 May 2024 16:37 by volodymyr.velyky

Tromp lambda diagram of an efficient Fibonacci calculator. Application bars adjusted from "alternative" style.

Input and output are Church-encoded natural numbers.

fib n == first (n next-pair (pair 0 1))

pair x y == \z.zxy

first p == p(\xy.x)

second p == p(\xy.y)

0 == \fx.x

1 == \fx.fx

plus m n == \fx.mf(nfx)

next-pair p == pair (second p) (plus (first p) (second p))

Put this in proper lambdas, and partially evaluate everything you can without n, and here we are. (copy)